A classic computer science problem - given a finite state machine and an infinite tape, how long can a program run ?
CatOnMat is an excellent resource, and I’ve followed it’s approach. You define e.g. a 2 state (a, b) machine like this:
a0 -> b1r a1 -> b1l
b0 -> a1l b1 -> h1r
where:
- if you’re in state A and read 0 from the tape, you change to state B, write 1 and move right.
- if you’re in state A and read 1 from the tape, you change to state B, write 1 and move left. … and so on.
That lasts for 6 steps:
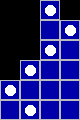
I then tried to iteratively figure out the best n-state beaver. The algorithm gave me grief for a couple of days, but I think I have got there. It’s also a much bigger problem space than I thought. I suspect there are some optimisations that I am missing.
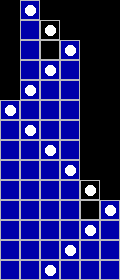
Best ones so far:
a0 -> c1r
a1 -> h0l
b0 -> b1l
b1 -> a1l
c0 -> c1l
c1 -> b0r

a0 -> b1r
a1 -> b1l
b0 -> a1l
b1 -> c0l
c0 -> h1r
c1 -> d1l
d0 -> d1r
d1 -> a0r
Gone through the examples on Wikipedia and I match as far as the 5 state (47 million steps in 14 seconds) - but too big to draw.
Oddity
I actually have a better 3 state machine than CatOnMat and Wikipedia ? Smells like a bug, but the other examples I have check out. They expect 3 state to peak at 14 steps; I have a 21 step … which checks out with the OpenSource example C code. Hmm.
a0 -> c1r
a1 -> h0l
b0 -> b1l
b1 -> a1l
c0 -> c1l
c1 -> b0r
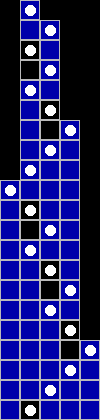
Got time for one more ?
This is the first 1000 steps of the 47 million step 5 state busy beaver.
